剑指offer——12. 矩阵中的路径

12. 矩阵中的路径

NowCoder

题目描述

判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向上下左右移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。

例如下面的矩阵包含了一条 bfce 路径。

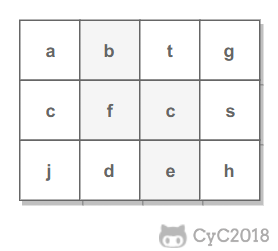
解题思路

使用回溯法（backtracking）进行求解，它是一种暴力搜索方法，通过搜索所有可能的结果来求解问题。回溯法在一次搜索结束时需要进行回溯（回退），将这一次搜索过程中设置的状态进行清除，从而开始一次新的搜索过程。例如下图示例中，从 f 开始，下一步有 4 种搜索可能，如果先搜索 b，需要将 b 标记为已经使用，防止重复使用。在这一次搜索结束之后，需要将 b 的已经使用状态清除，并搜索 c。

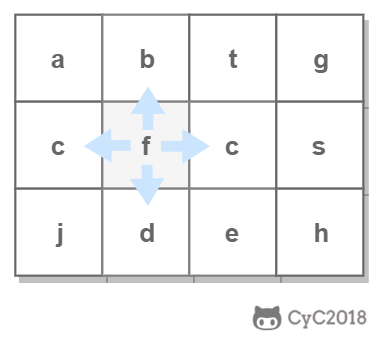
本题的输入是数组而不是矩阵（二维数组），因此需要先将数组转换成矩阵。

class Solution {
public:
    bool hasPath(vector<vector<char>>& matrix, string str) {
        if(matrix.empty() || matrix.at(0).empty()) return false;
        int row = matrix.size() - 1;
        int col = matrix.size() - 1;
        //轮循矩阵所有的元素
        for(int i = 0; i <= row; i ++ )
        {
            for(int j = 0; j <= col; j ++)
            {
                if(dfs(matrix, str, 0, i, j)) return true;
            }
        }
        return false;
    }
    
    /*
    matrix: 轮循的矩阵
    str:带查找的字符串
    strIndex：当前查找的str的下标
    x，y：当前查找的矩阵中的坐标
    **/
    bool dfs(vector<vector<char>>& matrix, string &str, int strIndex, int x, int y)
    {
        //--边界
        //判断当前字符是否相等
        if(str[strIndex] != matrix[x][y]) return false;
        //如果当前的字串匹配上 返回
        if(strIndex == str.size() - 1) return true;
        //--当前字符匹配，查找下一个字符
        char t = matrix[x][y]; //记录当前的字符 用于回溯
        matrix[x][y] = t + 1;//t + 1; //'*' //避免回溯重复查找 用一个特殊字符或者改变值
        //定义方向变量  用于四个反向 左下右上 
        int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, -1, 0, 1};
        for(int i = 0; i < 4; i++ )
        {
            int a = x + dx[i],  b = y + dy[i];
            if(a >= 0 && a < matrix.size() && b >= 0 && b < matrix[0].size())
                if(dfs(matrix, str, strIndex + 1, a, b)) return true;  //找到结果即返回
        }
        //--恢复数据 没有找到 切换下一个点
        matrix[x][y] = t ;  //回溯
        return false;
    }
};

java 实现

class Solution {
    public boolean exist(char[][] board, String word) {
        if(board.length==0 || board[0].length == 0 || word == null) {
            return false;
        }
        int row = board.length;
        int col = board[0].length;
        boolean[][] vis = new boolean[row][col];
        // 遍历矩阵
        for(int i = 0; i < row; i ++) {
            for(int j = 0; j < col; j ++) {
                if(dfs(board, i, j, word, 0, vis)) {
                    return true;
                }
            }
        }
        return false;
    }
   

    boolean dfs(char[][] board, int x, int y, String word, int u, boolean[][] vis) {
        // 当前矩阵和数组字符不同 返回FALSE；当字符串匹配完成，返回true
        if(word.charAt(u) != board[x][y]) {
            return false;
        }
        if(u == word.length() - 1) {
            return true;
        }
        
        // 防止重复
        vis[x][y] = true;
        int dx[] = {-1, 0, 1, 0};
        int dy[] = {0, -1, 0, 1};
        // 遍历四个方向 左下右上
        for(int i = 0; i < 4; i ++) {
            int nx = dx[i] + x;
            int ny = dy[i] + y;
            if(nx >= 0 && nx < board.length && ny >= 0 && ny < board[0].length && !vis[nx][ny]) {
                if(dfs(board, nx, ny, word, u+1, vis)) {
                    return true;
                }
            }
        }
        vis[x][y] = false;
        return false;
    }
}

无需状态数组：

class Solution {
    public boolean exist(char[][] board, String word) {
        if(board.length==0 || board[0].length == 0 || word == null) {
            return false;
        }
        int row = board.length;
        int col = board[0].length;
        // 遍历矩阵
        for(int i = 0; i < row; i ++) {
            for(int j = 0; j < col; j ++) {
                if(dfs(board, i, j, word, 0)) {
                    return true;
                }
            }
        }
        return false;
    }
   

    boolean dfs(char[][] board, int x, int y, String word, int u ){
        // 当前矩阵和数组字符不同 返回FALSE；当字符串匹配完成，返回true
        if(word.charAt(u) != board[x][y]) {
            return false;
        }
        if(u == word.length() - 1) {
            return true;
        }
        
        // 防止重复
        char t = board[x][y];
        board[x][y] = '*';
        int dx[] = {-1, 0, 1, 0};
        int dy[] = {0, -1, 0, 1};
        // 遍历四个方向 左下右上
        for(int i = 0; i < 4; i ++) {
            int nx = dx[i] + x;
            int ny = dy[i] + y;
            if(nx >= 0 && nx < board.length && ny >= 0 && ny < board[0].length) {
                if(dfs(board, nx, ny, word, u+1)) {
                    return true;
                }
            }
        }
        board[x][y] = t;
        return false;
    }
}