10.3 跳台阶

题目链接

NowCoder

题目描述

一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

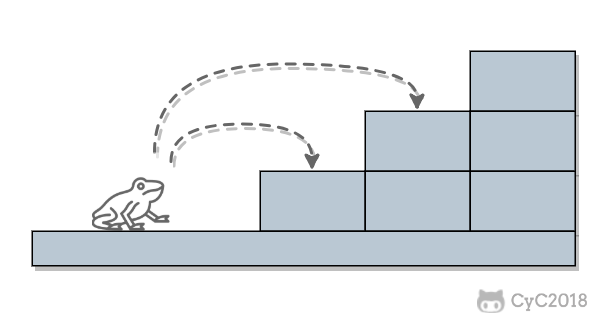
解题思路

当 n = 1 时，只有一种跳法：

当 n = 2 时，有两种跳法：

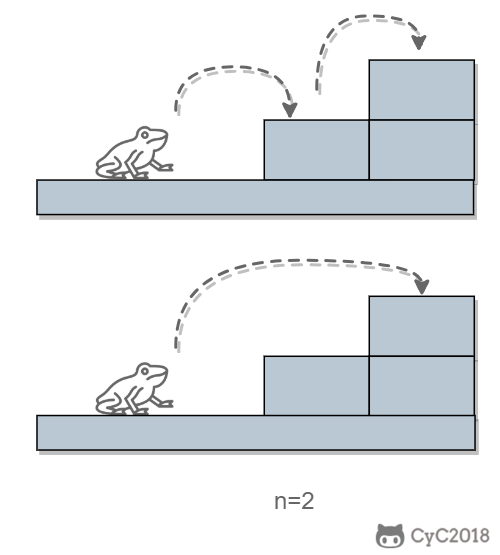
跳 n 阶台阶，可以先跳 1 阶台阶，再跳 n-1 阶台阶；或者先跳 2 阶台阶，再跳 n-2 阶台阶。而 n-1 和 n-2 阶台阶的跳法可以看成子问题，该问题的递推公式为：

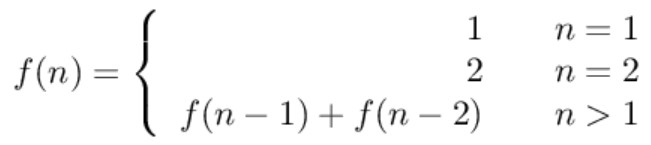
class Solution {
public:
    int jumpFloor(int n) {
        int f=1,g=2;
        n--;
        while(n--)
        {
            g+=f;
            f=g-f;
        }
        return f;
    }
};

java实现

设跳上 nn 级台阶有 f(n)f(n) 种跳法。在所有跳法中，青蛙的最后一步只有两种情况：跳上 11 级或 22 级台阶。
当为 11 级台阶：剩 n-1n−1 个台阶，此情况共有 f(n-1)f(n−1) 种跳法；
当为 22 级台阶：剩 n-2n−2 个台阶，此情况共有 f(n-2)f(n−2) 种跳法。
f(n)f(n) 为以上两种情况之和，即 f(n)=f(n-1)+f(n-2)f(n)=f(n−1)+f(n−2) ，以上递推性质为斐波那契数列。本题可转化为求斐波那契数列第 nn 项的值，与面试题10- I. 斐波那契数列等价，唯一的不同在于起始数字不同。
青蛙跳台阶问题： f(0)=1f(0)=1 , f(1)=1f(1)=1 , f(2)=2f(2)=2 ；
斐波那契数列问题： f(0)=0f(0)=0 , f(1)=1f(1)=1 , f(2)=1f(2)=1 。

作者：jyd
链接：https://leetcode-cn.com/problems/qing-wa-tiao-tai-jie-wen-ti-lcof/solution/mian-shi-ti-10-ii-qing-wa-tiao-tai-jie-wen-ti-dong/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

class Solution {
    public int numWays(int n) {
        if(n <=1) return 1;
        // f(n) = f(n-1) + f(n-2)

        int a = 1; // n=0 >1
        int b = 1; // n=1 > 1
        for(int i = 2; i <=n; i++) {
            int tmp = b;
            b = a+b;
            a = tmp;
            if(b > 1000000007 ) b %= 1000000007;
        }
        return b;
    }
}